2023. 8. 5. 17:11ㆍ자료 구조 및 알고리즘
DFS : DEPTH First Search (깊이 우선 탐색)
그래프 전체를 완벽하게 탐색하는 방법 중 하나이다.
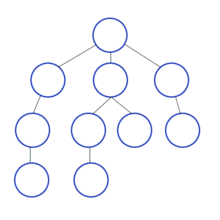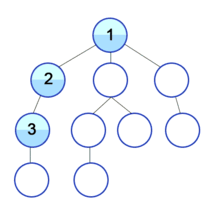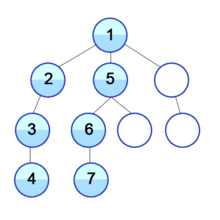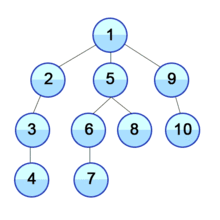
위 그림과 같이 현재 정점에서 갈 수 있는 점들까지 들어가면서 탐색한다.
장점 :
1. 저장공간의 수요가 비교적 적다.
2. 목표 노드가 깊은 단계에 있을 경우 해를 빨리 구할 수 있다.
단점 :
해가 없는 경로에 깊이 빠질 가능성이 있다.
얻어진 해가 최단 경로일 보장이 없다.
구현 방법 :
[재귀함수]나 [스택]으로 구현한다.
노드 방문 시 방문 여부를 저장하고 검사해야 한다.
구현 단계 :
1. 시작 노드를 스택에 삽입 및 방문 처리
2. 작은 수부터 탐색 규칙에 따라 탐색을 진행
3. 다음 노드를 방문처리하고 이미 방문한 노드는 무시, 방문하지 않은 노드는 스택에 넣기
4. 반복하다가 더 이상 반복할 수 없는 노드에 도달하게 되면 pop()을 진행
5. 반복 진행하여 모든 노드를 탐색하낟.
구현 예제 :

#include <iostream>
#include<vector>
//stack이 아닌 vector을 이용하는 이유
//밑에 25줄에서 vector 안에 있는 값을 참조할건데
//stack은 참조가 안되지만 vector는 가능하다.
using namespace std;
//방문 처리 배열 (전부 다 0으로 초기화 되어있음)
bool visited[9];
//스택 배열 생성
vector<int> graph[9];
void dfs(int x)
{
//매개변수의 값인 노드를 들렸다는 뜻
visited[x] = true;
//값 출력하기 위한 문장
cout << x << " ";
for (int i = 0; i < graph[x].size(); i++)
{
int y = graph[x][i];
if (!visited[y])
dfs(y);
}
}
int main(void)
{
graph[1].push_back(2);
graph[1].push_back(3);
graph[1].push_back(8);
graph[2].push_back(1);
graph[2].push_back(7);
graph[3].push_back(1);
graph[3].push_back(4);
graph[3].push_back(5);
graph[4].push_back(3);
graph[4].push_back(5);
graph[5].push_back(3);
graph[5].push_back(4);
graph[6].push_back(7);
graph[7].push_back(2);
graph[7].push_back(6);
graph[7].push_back(8);
graph[8].push_back(1);
graph[8].push_back(7);
dfs(1);
return 0;
}

BFS : Breadth First Search (깊이 우선 탐색)
Dfs와 같이 그래프 전부를 탐색하는 방법 중 하나이다.

위 그림과 같이 시작 노드를 방문하여 인접한 모든 노드들을 먼저 방문하는 방법
(최단 경로 탐색 or 임의의 경로 탐색)
장점 :
1. 출발노드에서 목표 노드까지의 최단 길이 경로를 보장
단점 :
1. 경로가 매우 길 경우에는 탐색 가지가 급격히 증가함에 따라 많은 기억 공간을 필요로 한다.
구현 방법 :
[큐]를 이용 구현한다.
노드 방문 시 방문 여부를 저장하고 검사해야 한다.
구현 단계 :
1. 시작 노드를 큐에 삽입 후에 방문 처리한다.
2. 시작 노드를 꺼내고, 인접 노드들을 큐에 넣은 뒤 방문 처리한다.
3. 큐의 앞 부분을 꺼내고, 2번 행위를 반복한다.
4. 큐가 비어질 때까지 반복한다.
구현 예제 :

#include <iostream>
#include <vector>
#include <queue>
//stack이 아닌 vector을 이용하는 이유
//밑에 25줄에서 vector 안에 있는 값을 참조할건데
//stack은 참조가 안되지만 vector는 가능하다.
using namespace std;
//방문 처리 배열 (전부 다 0으로 초기화 되어있음)
bool visited[9];
//스택 배열 생성
vector<int> graph[9];
void bfs(int start)
{
//큐를 선언하고 첫 노드를 먼저 넣어준다.
queue<int> q;
q.push(start);
//매개변수의 값인 노드를 들렸다는 뜻 (첫 노드를 방문 처리)
visited[start] = true;
while (!q.empty())
{
//첫 노드 뽑기
int x = q.front();
q.pop();
//출력
cout << x << " ";
//주변 노드 모두 방문, 방문하지 않았다면 큐에 넣고 방문 처리
for (int i = 0; i< graph[x].size(); i++)
{
int y = graph[x][i];
if(!visited[y])
{
q.push(y);
visited[y] = true;
}
}
}
}
int main(void)
{
graph[1].push_back(2);
graph[1].push_back(3);
graph[1].push_back(8);
graph[2].push_back(1);
graph[2].push_back(7);
graph[3].push_back(1);
graph[3].push_back(4);
graph[3].push_back(5);
graph[4].push_back(3);
graph[4].push_back(5);
graph[5].push_back(3);
graph[5].push_back(4);
graph[6].push_back(7);
graph[7].push_back(2);
graph[7].push_back(6);
graph[7].push_back(8);
graph[8].push_back(1);
graph[8].push_back(7);
bfs(1);
return 0;
}

그래프의 모든 정점을 방문하는 것이 주요한 문제일 경우
=> DFS와 BFS 둘 다 사용하면 됨
경로의 특징을 저장해야 하거나 검색 대상 규모가 큰 문
=> 각 정점에 숫자가 적혀 있고 a부터 b까지 가는 경로를 구하는데
같은 숫자가 있으면 안된다는 문제들은 DFS를 사용하면 됨
최단거리를 구하거나 검색 대상 규모가 크지 않고 시작 대상에서 원하는 대상이 멀지 않다면
=> BFS를 사용하면 됨
'자료 구조 및 알고리즘' 카테고리의 다른 글
| 그리디 알고리즘 (Greedy Algorigthm) (0) | 2023.08.27 |
|---|---|
| 이진 탐색 (Binary Search) (0) | 2023.08.16 |
| 자료 구조 그래프 (0) | 2023.07.25 |
| Dynamic Programming (동적 계획법) (0) | 2023.07.18 |
| 자료 구조 Heap와 구현하기 (C++) (0) | 2023.07.06 |